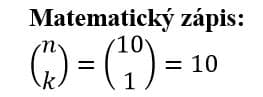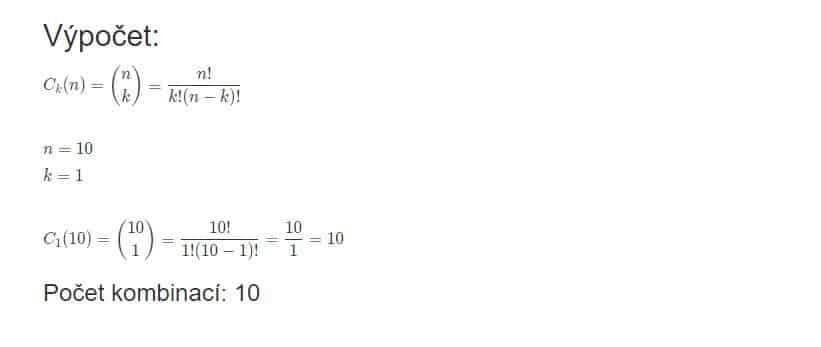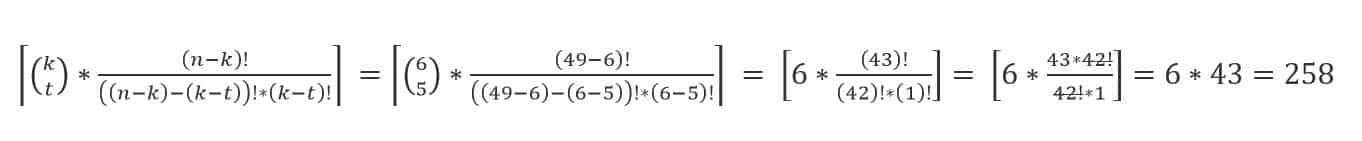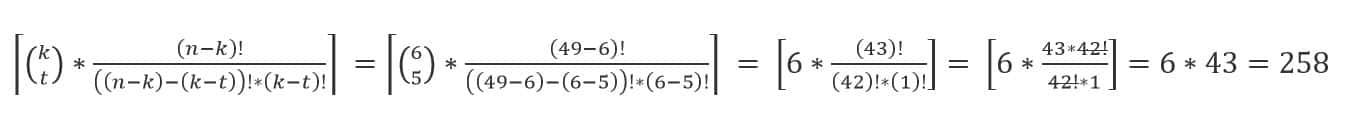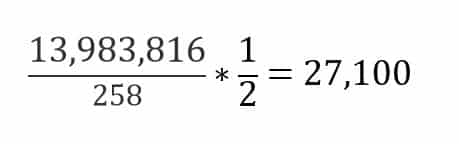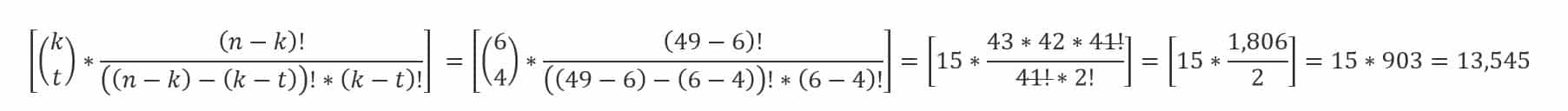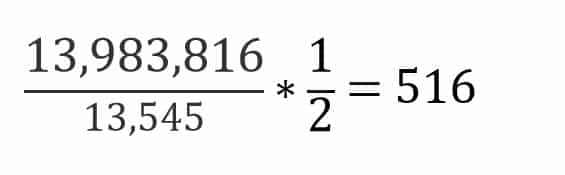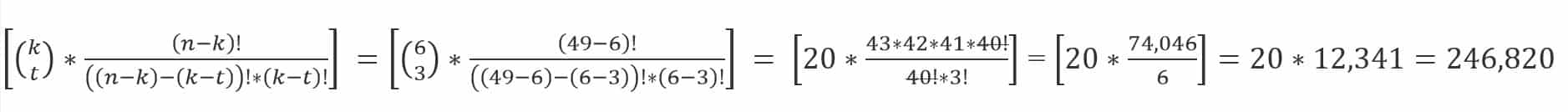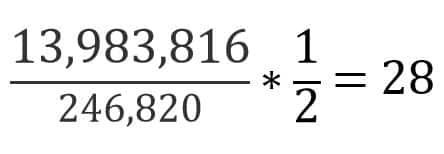Ve výpočtu prvního pořadí máme obrázek, který nám odhaluje kombinatorický vzorec, díky kterému se dopočítáme k celkovému počtu číselných kombinací, které lze při slosování vytáhnout z osudí. Pojďme si spolu tento vzorec trochu rozebrat, aby pro tebe byl výpočet co možná nejpřehlednější.
Důležité informace, které před začátkem výpočtu musíš mít na paměti:
- ve vzorci najdeš symbol vykřičníku (!), který se nazývá faktoriál
- faktoriál vyjadřuje součin všech přirozených čísel menších nebo rovných danému číslu
(5! – „pět faktoriál“ je rovno 5 × 4 × 3 × 2 × 1 = 120)
- faktoriál vyjadřuje součin všech přirozených čísel menších nebo rovných danému číslu
- čísla stejné hodnoty, která se nachází v horní i spodní polovině zlomku (v čitateli i jmenovateli) se mezi sebou krátí = „zmizí“ ze zápisu
V původním vzorci vidíš ve vrchní polovině zlomku (v čitateli) „49!“ – to znamená, že toto číslo musíš rozepsat jako 49 × 48 × 47 × … 1.
Ve spodní polovině zlomku (ve jmenovateli) vidíš „6! (49-6)!“ – v tomto případě tedy prvně vypočítáš závorku a následně pokračuješ s výpočtem. Po vypočítání závorky ti ve jmenovateli zůstane „7! 43!“ – i tato čísla musíš kvůli faktoriálu roznásobit, a to od jejich hodnoty až po jedničku. Zápis tedy bude vypadat 7 × 6 × 5 × 4 × 3 × 2 × 1 × 43 × 42 × 41 × … 1.
Když máš pečlivě rozepsaného čitatele i jmenovatele tak zjistíš, že se násobení od 43 níže opakuje jak v čitateli, tak ve jmenovateli. V tuto chvíli se tedy obrať na druhou odrážku a pravidlo, které jsme si v ní řekli → stejná čísla se krátí. Toto pravidlo tě následně dovede k zápisu, který vidíš na obrázku v článku a to „49 × 48 × 47 × 46 × 45 × 44 lomeno 6 × 5 × 4 × 3 × 2 × 1“.
No, a pak už stačí jen čísla mezi sebou vynásobit a hned zase vydělit a máš výsledek, který vidíš na obrázku i v textu, a to, že z čísel od 1 do 49 dokážeš vytvořit 13 983 816 unikátních šestic.